The Brachistochrone

Say you have two points A and B on a flat cartesian plane and there’s a point particle at point A experiencing a force of gravity downwards. What is the path that that point particle could take to get from point A to point B in the shortest amount of time. One would think a straight line would be the answer to this question as the shortest path between two points is a straight line. However, a straight line would cause the point particle to experience a linear change in velocity over time, not a very great way to gain speed. One would then think that perhaps a steep drop would be better as the steeper the curve is the greater the change of gravitational potential energy to kinetic energy, thus causing a greater change in velocity over time. Yet an extremely steep path would have a greater length than one that is less steep, making the time taken to get from point A to point B longer. One can then see hints implying that one must find a balance between steepness and shortness for the path to reach some path, some curve that minimizes time. It turns out the shortest path is a curve called a brachistochrone, the curve coloured red in the image below being a brachistochrone.

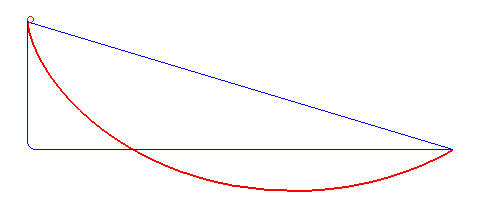
[1]

This curve was discovered by several people in the late 1700s , being the answer to a challenge posed by Johann Bernoulli, a mathematician, to the mathematicians of Europe at that time: Newton, Jacob Bernoulli, Ehrenfried Von Tschirnhaus, Gottfried Wilhelm Von Leibniz, etc. An interesting solution developed by Johann Bernoulli to this challenge was through Fermat’s principle  and Snell’s Law. Fermat’s principle states that if a beam of light travels from point A to B, it does so along the fastest path possible. Snell’s Law states that the sine of the angles for refracted light beam over the respective speeds of light in those mediums stays constant, as light moves from one medium to the next.

[2]

One must imagine light passing through different mediums of the same size at different heights on a plane, the speed of light in each medium increasing as the height decreases. By conservation of energy, one can find that v, the velocity of the light in each medium  is equal to the square root of 2 times the acceleration due to gravity times the height of that light if one imagines the light like a ball sliding  down a curve. One must then imagine that there exists an infinite number of mediums, each following conservation of energy. From that, one receives the Brachistochrone.

Credits to Wikipedia for image [1]

Credits to Charged Magazine for image [2]

Credits to 3blue1brown and Steven Strogatzs’ discussion concerning the brachistochrone

https://www.youtube.com/watch?v=Cld0p3a43fU